通信原理期末复习

第一章 绪论

通信性能指标：

信息量：消息x所含的信息量I是x发生的概率的函数 $I(x)=-\log_2(P(x))$ 单位 bit

信息传输速率：

• 传码率$R_B$：单位时间内传输码元（可以是二进制、多进制）的个数，单位 Baud/s

• 传信率$R_b$：单位时间内传输的比特总数，单位 bit/s或bps

• 关系：$R_b =R_B \log_2M$ 其中 M 为进制数

频带利用率（2种表示方式，B为信号传输占用的带宽）：

• $\eta=\frac{R_B}{B} ~~(Baud/Hz)$
• $\eta_b=\frac{R_b}{B} ~~(bit/s/Hz)$

误码率：

• 码元差错率：$P_e=\frac{错误码元数}{传输的总码元数}$
• 信息差错率：$P_e=\frac{错误比特数}{传输的总比特数}$

第二章 随机信号与噪声分析

随机过程X(t)的数字特征

• 数学期望：$E[X(t)]=\int_{-\infty}^{+\infty}x f(x, t)dx$

• 方差：$D[X(t)] = E\{[X(t)-a(t)]^2\}$ 其中a(t)为数学期望

• 自相关函数（重要）：$R(t_1, t_2)=E[X(t_1)X(t_2)]$

• 协方差函数：$B(t_1, t_2)=E\{[X(t_1)-a(t_1)][X(t_2)-a(t_2)]\}$，

  且 $B(t_1, t_2)=R(t_1, t_2)-a(t_1)a(t_2)$ (重要)

平稳随机过程

广义平稳：

• 均值与时间t无关，为常数$a$
• 自相关函数只与时间间隔有关，为$R(\tau)$

狭义平稳：

• 一维情况：的概率密度函数与时间t无关

判断 $X(t)=A\cos(\omega t+φ)$ 的平稳性，其中A和ω为常数，φ服从【均匀分布】，则

• $E[X(t)]=0$
• $R_X(t_1,t_2)=\frac{A^2}{2}\cos\omega \tau$，其中 $\tau=t_2-t_1$

综上：X(t)是广义平稳的

【平稳随机过程的各态历经性】：

假设 x(t) 是平稳随机过程 $X(t)$ 的任意一次实现，则其时间均值、时间相关函数分别为：

• 时间均值：$\overline{a}=\lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2} x(t)dt$
• 时间相关函数：$\overline{R(\tau)}= \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} x(t)x(t+\tau)dt$

如果平稳过程使得下式成立：

• $a=E[X(t)]=\overline{a}$
• $R(\tau)=\overline{R(\tau)}$

则该平稳随机过程具有各态历经性

【自相关函数的性质】：

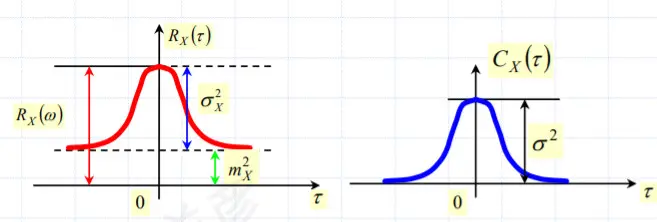
记住这幅图就可以记住 $R(\tau)$ 的性质(拿随机信号处理的PPT的图来顶一下😅)

• $R(\tau)$ 为偶函数
• $R(0)=E[X^2(t)]=\sigma^2 + E^2(\infty)$ 图中的 $\sigma_X^2$ 即方差， $m_X^2$ 即 $E^2(\infty)$
• $R(0)$为平均功率， $\sigma^2$为交流功率， $E^2(\infty)$ 为直流功率

【功率谱密度函数$P_X(\omega)$】

• 确定信号：$P_x(\omega)=\lim_{T\to \infty} \frac{|X_T(\omega)|^2}{T}$

• 随机信号：$P_X(\omega)= E[P_x(\omega)] = \lim_{T\to \infty} \frac{E[|X_T(\omega)|^2]}{T}$

性质：自相关函数的傅里叶变换等于 $P_X(\omega)$，即 $R(\tau)\Leftrightarrow P_X(\omega)$

• $P_X(\omega)$ 是确定函数，偶函数，非负函数

• 随机过程的平均功率=$R(0)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} P_X(\omega) d\omega$

第三章 信道与噪声

香农公式：

信道容量：$C=B\log_2(1+S/N)$ (bit/s)

第四章 模拟调制系统

幅度调制

• 普通调幅AM

  $s_{AM}(t)=[A_0+m(t)]\cos \omega_ct$ 其中m(t)为输入的调制信号，输出$s_{AM}(t)$ 为【调幅信号】，所以经过调制的信号都可称为 【已调信号】

  调幅度：$\frac{\max(m(t))}{A_0}$ 调幅度小于等于 1 时可以采用包络检波

• 双边带调幅DSB

  $s_{DSB}=m(t)\cdot \cos(\omega_ct)$

• 单边带调制（调制结果分为上边带、下边带两种）

  • 上边带：$s_{USB}=\frac{1}{2}m(t)\cos(\omega_ct)-\frac{1}{2}\hat{m}(t)\sin(\omega_ct)$

  • 下边带：$s_{LSB}=\frac{1}{2}m(t)\cos(\omega_ct)+\frac{1}{2}\hat{m}(t)\sin(\omega_ct)$

    注：$\hat{m}(t)$ 是 $m(t)$ 的希尔伯特变换，即 m(t) 的正频率部分相位减去 $\frac{\pi}{2}$

    

带宽：$B_{AM}=B_{DSB}=2B_{SSB}=2B_{VSB}$

功率：设 $P_m$为调制信号 $m(t)$ 的平均功率$E(m^2(t))$，则

• $P_{AM}=载波功率+边带功率=P_c+P_s=\frac{A_0^2}{2}+\frac{P_m}{2}$
• $P_{DSB}=P_s=\frac{P_m}{2}$
• $P_{SSB}=\frac{1}{2}P_s=\frac{1}{4}P_m$

调制效率：${\Large \eta_{AM}=\frac{P_s}{P_{AM}}}$

解调：

• AM解调：

  • 相干解调：$m_o(t)\approx \frac{1}{2}[m(t)+A_0]\overset{隔直}{\rightarrow} \frac{1}{2}m(t)$
  • 包络检波：$m_o(t)\approx m(t)+A_0\overset{隔直}{\rightarrow} m(t)$

• DSB解调：

  相干：$m_o(t)=\frac{1}{2}m(t)$ 输出功率：$P_o=\frac{1}{4}\overline{m^2(t)}=\frac{1}{4}P_m$

• SSB解调：

  相干：$m_o(t)=\frac{1}{4}m(t)$， $P_o=\frac{1}{16}\overline{m^2(t)}=\frac{1}{16}P_m$

解调器的信噪比增益：

• $G_{AM}\le 1$ (包络检波、且为大信噪比时)，单音调制，且调制度=100%时，$G_{AM}=2/3$
• $G_{DSB}=2$
• $G_{SSB}=1$

平稳高斯白噪声 $n_i(t)$ 通过解调器后，输出 $n_o(t)=n_i(t)/2$，因此输出噪声功率 $N_o=N_i/4$

通常高斯白噪声的[双边]功率谱 $\frac{n_0}{2}$ W/Hz，[单边]功率谱为 $n_0$ W/Hz

角度调制

调角信号：$s_{m}(t)=A_0\cos(\omega_ct+\varphi(t))$

• 调相：$\varphi(t)=K_P m(t)$
• 调频：$\frac{d\varphi(t)}{dt}=K_F m(t)$

调频带宽：$B_{FM}=2(D+1)f_m$ ，其中 $f_m$ 为调制信号m(t)的最高频率

• 窄带调频时，$D<<1, B_{NBFM}=2f_m$
• 宽带调频时，$B_{FM}=2(D+1)f_m$
  • D为调频指数，$D=\Delta f_m/f_m$， $\Delta f_m=K_F|m(t)|_{\max}$ 为最大频偏，单音调制时用 $m_f$代替 D

功率：窄带、宽带均为 $P_{FM}=载波功率=A_0^2/2$

调频信号的解调：

• 非相干解调 $m_o(t)=K_dK_Fm(t)$
• 相干解调：$m_o(t)=\frac{1}{2}A_0K_Fm(t)$

信噪比增益：$G_{FM}=3m_f^2(m_f+1)\approx 3m_f^3$

第五章 数字基带传输系统

各种编码

• 单极性不归零码

• 双极性不归零码

• 单极性归零码

• 双极性归零码

• AMI码（传号反转码，1码交替用正、负电平表示，0码用低电平表示）

• HDB3码（解决AMI码中连0长串问题）

  1	原码->AMI码->加V（交替正负）->加B（与后一个V正负相同）->±V、±B改为±1

  

数字基带传输

数字基带信号功率谱：

\begin{align} &P_s(f)\\ &=P_u(f)+P_v(f)\\ &=f_bP(1-P)|G_1(f)-G_2(f)|^2+\\&\sum_{m=-\infty}^{+\infty}[ f_b^2|PG_1(mf_b)+(1-P)G_2(mf_b)|^2\delta(f-mf_b)] \end{align}

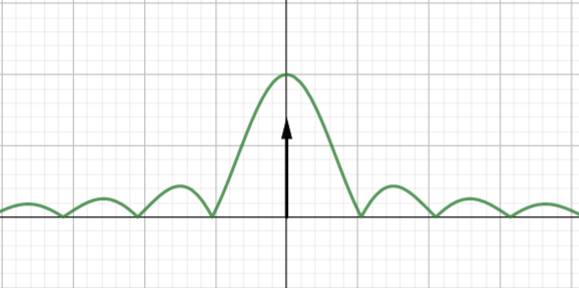
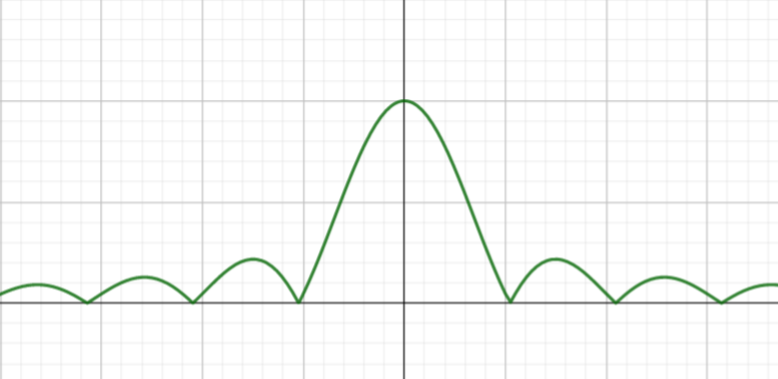
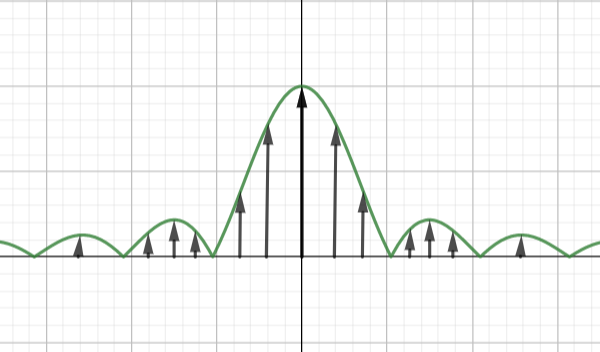
单极性NRZ(含直流分量)	双极性NRZ(0,1等概发送)	单极性RZ(含离散分量)	双极性RZ(0,1等概发送)

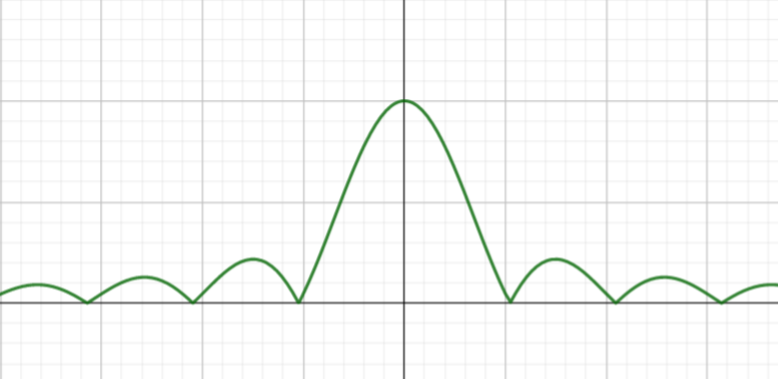无码间干扰

无码间干扰最大速率：$R_B=\frac{2}{1+\alpha}f_{ch}$ ，$f_{ch}$为系统最高截止频率

最大码速时的频带利用率：$\eta=\frac{2}{1+\alpha}$ (Baud/Hz)

无码间干扰的误码率：

• 双极性、等概率发送0，1：$P_e=\frac{1}{2}erfc(\frac{A}{\sqrt{2}\sigma_n})$
• 单极性、等概率发送0，1：$P_e=\frac{1}{2}erfc(\frac{A}{2\sqrt{2}\sigma_n})$

部分响应系统

特点：频带利用率可以达到 2 Baud/Hz

实现方式：

1. 预编码：$b_k=a_k\oplus b_{k-1}$
2. 相关编码（消除误码传播）：$c_k=b_k+b_{k-1}$
3. 译码：$a_k=b_k\oplus b_{k-1}=[c_k]_{\mod{2}}$

均衡器

输出：

$$y_k=\sum_{i=-N}^N C_ix_{k-i}$$

第六章 数字信号频带传输

主要介绍如何将数字信号调制到高频范围进行传输

带宽

• $B_{2ASK}=2R_B$
• $B_{2FSK}=|f_1-f_2|+2R_B$
• $B_{2DPSK}=B_{2PSK}=2R_B$

误码率

相干解调

• 2ASK: $\frac{1}{2}erfc(\sqrt{\frac{r}{4}})$, r>>1时，$\frac{1}{\sqrt{\pi r}} e^{-r/4}$
• 2FSK: $\frac{1}{2} erfc(\sqrt{\frac{r}{2}})$, r>>1时，$\frac{1}{\sqrt{2\pi r}} e^{-r/2}$
• 2PSK: $\frac{1}{2}erfc(\sqrt{r})$, r>>1时，$\frac{1}{2\sqrt{\pi r}} e^{-r}$
• 2DPSK: $erfc(\sqrt{r})$, r>>1时，$\frac{1}{\sqrt{\pi r}} e^{-r}$
• 4PSK: $erfc(\sqrt{r}\sin\frac{\pi}{4})$
• 4DPSK: $erfc(\sqrt{2r}\sin\frac{\pi}{8})$

非相干解调

• 2DPSK（差分相干解调）: $\frac{1}{2}e^{-r}$
• 2FSK（包络检波）: $\frac{1}{2}e^{-r/2}$
• 2ASK（包络检波）: $\frac{1}{2}e^{-r/4}$

解调框图

…

第七章 现代数字调制技术

主要看书，了解基本目的和原理

QAM：带宽、频率利用率记一下即可

第八章 模拟信号的数字传输

主要介绍模拟信号如何转换为数字信号：采样、量化、编码

采样定理

$f_s=2f_m$

了解一下理想采样、自然采样、平顶采样

带通抽样定理

采样角频率：

$$\omega_s=2W(1+\frac{M}{N})$$

其中

• $N= floor(\omega_H/W)$，也就是 $\omega_H/W$的整数部分
• $M=\frac{\omega_H}{W}-N$, 且 $0\le M < 1$

最终 $2W<\omega_s<4W$

量化

均匀量化：

• 最小量化间隔：$\Delta A=\frac{b-a}{M}$，最大值b，最小值a，M个量化区间
• 最大量化误差：$(\Delta q)_{\max}=\Delta A/2$
• 量化信噪比：$\frac{S_o}{N_o}=M^2$

非均匀量化：

A律压缩曲线：

$$y=\begin{cases} \frac{Ax}{1+\ln A} & 0<x\le \frac{1}{A} \\ \frac{1+Ax}{1+\ln A} & \frac{1}{A} < x\le 1 \end{cases}$$

采用13折线编码：A=87.6

量化信噪比：

• 大信噪比时：$\frac{S_o}{N_o}=2^{2N_b},N_b\ge \log_2M$
• 小信噪比时：$\frac{S_o}{N_o}=\frac{1}{4P_e}$, Pe为误码率

PCM编码

十三折线编码基本步骤

例题：对抽样值1268进行量化编码

编码结果是一个8位码 $b_7b_6b_5b_4b_3b_2b_1b_0$

• 符号位 $b_7$：1-正，0-负；1268为正数，则$b_7=1$

• 段落码 $b_6b_5b_4$：根据下表判断该取哪个值，比如，抽样值为567，则$512\le567<1024$，则$b_6b_5b_4=110$。抽样值为1268>1024，则$b_6b_5b_4=111$

  抽样值	$b_6b_5b_4$
  1024	111
  512	110
  256	101
  128	100
  64	011
  32	010
  16	001
  0	000

• 段内码 $b_3b_2b_1b_0$：将对应区间分成均匀分为16份，比如抽样值为567，所在区间为[512, 1024)，分成16份，每份大小为(1024-512)/16=32；题中给的抽样值 1268>1024，因此1268所在的区间为[1024, 2048)，每份大小ΔA=(2048-1024)/16=64，则

  0000对应1024

  0001对应1024+64*1

  0010对应1024+64*2，

  …

  1111对应1024+64*15

• 因为 1024+64*3=1216 < 1268 < 1024+64*4=1280，因此1268对应的 $b_3b_2b_1b_0=0011$

• 综上，得到最终编码为 11110011

• 误差计算

  • 采用起始电平为译码电平时，则实际上11110011对应1216，因此 误差=1268-1216=52
  • 通常采用中间电平为译码电平，即在原来的基础上加 ΔA/2，则1110011对应译码后应该为 1216+64/2=1248，因此最终【误差】=1268-1248=20

时分复用TDM

• $f_s=2f_m$, $T_s=\frac{1}{2f_m}$
• 每个0、1信号占用时间：$T_b=\frac{T_s}{N_b n}$, n代表几路信号进行复用
• $R_B=1/T_b$
• 无码间干扰带宽：$B=R_B/2$
• 主瓣带宽：$B=1/\tau$，τ表示码元宽度

不采用时分复用时：$R_B=N_bf_s$

第九章 差错控制编码

基本概念

码重：一个码中1的个数，如0011码重为2

对2个码求异或的结果中1的个数，即码距$d_0$，如 0011+1000=1011，码距为3

检错与纠错的条件

• $d_0\ge e+1$，可以检错e个码
• $d_0\ge 2t+1$，可以纠错t个码
• $d_0\ge t+e+1且e\ge t$，可以检查出e个错，同时纠正其中t个错

线性分组码

对于一个(n, k)码，即n个码中有k个是信息码，r=n-k个监督码

• 其编码效率为 $k/n$

• 监督矩阵 $H_0=[P~~~I_r]$，其中 $I_r$代表单位矩阵，阶数为r，H0共n列，r行。（注：H0是典型化的矩阵，不是典型化需要进行【矩阵初等变化】，才能得到典型化的矩阵）

• 生成矩阵 $G_0=[I_k~~~P^T]$，其中 $I_k$代表单位矩阵，阶数为k，G0共n列，k行。（注：G0是典型化的矩阵，不是典型化需要进行【矩阵初等变化】，才能得到典型化的矩阵）

发送时使用的码组（系统码）：$A=[a_{n-1}a_{n-2}\cdots a_{n-k}]\times G_0$

【译码方式】

计算校正子 $S^T=HR^T$，$R^T$为接收码组的列向量

$|S^T|-1=j$，则 R 中从又往左数（0开始）第j个码发生错误，记得在回答时纠正过来

循环码

生成多项式 g(x) 的确定

• g(x)最高次项为 $x^{n-k}$，常数项为1
• 一般题目会给出许用码组，在许用的码组中找出一个码字，其中 $a_{n-k}$左边的码均为0，第n-k个码$a_{n-k}$为1，最右边的码$a_0$为1，然后根据这个码的$a_1,a_2,\cdots,a_{n-k-1}$来判断$g_1,g_2,\cdots,g_{n-k-1}$是多少。

证明g(x)是循环码(n,k)的生成多项式

• 即证 $x^n-1$ 能被 $g(x)$ 整除

求码多项式A(x)

• 先求监督多项式 $r(x)\equiv x^{n-k}m(x)，模g(x)$

• 则 $A(x)=m(x)x^{n-k} + r(x)$

  m(x)为信息码多项式

判断接收到的码多项式 $R(x)$ 是不是码多项式

• 利用所有码多项式均能被 g(x) 整除的性质

译码：$S^T=HR^T$ 或 $S=RH^T$

第十章 数字信号的最佳接收

最大信噪比准则与匹配滤波器

• 输出噪声功率谱 $P_{no}(\omega)=\frac{n_o}{2}|H(\omega)|^2$, $n_0/2$是输入高斯白噪声的功率谱密度函数$P_{ni}$
• 输出噪声总功率 $N_o=\frac{1}{2\pi}\int_{-\infty}^{+\infty}P_{no}(\omega)d\omega$
• 输入信号功率 $E_i=\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_i(\omega)|^2d\omega$
• 最大输出信噪比 $r_{omax}=\frac{E_i}{n_0/2}$

根据 $s_i(t)$ 计算匹配滤波器系统函数和冲击响应函数

• $h(t)=Ks_i(t_0-t)$，通常取 $K=1, t_0=T_b$
• $H(\omega)=KS_i^*(\omega)e^{-j\omega t_0}$

输出信号计算： $s_o(t)=KR_{s_i}(t_0-t)$

匹配滤波器结构

最小误码率准则与相关接收机

判决准则

$P(s_1)P(x|s_1)>P(s_2)P(x|s_2)$ 则判断为s1, 否则为s2，相等时无法判断，误码率最大

相关接收机结构

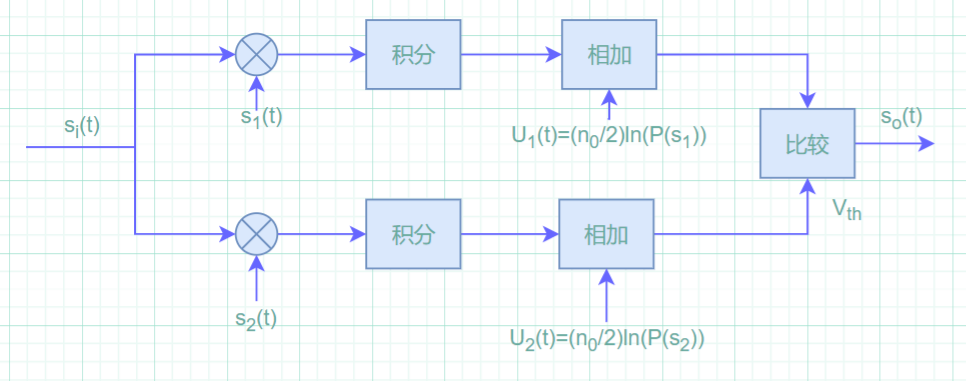
最佳接收机误码率

$P_e=\frac{1}{2}erfc(\sqrt{\frac{E_b(1-\rho)}{2n_0}})$

其中，两个信号平均能量$E_b=\frac{1}{2}\int_{0}^{T}(s_1^2(t)+s_2^2(t))dt$

相关系数 $\rho=\frac{\int_0^Ts_1(t)s_2(t)dt}{E_b}$

• 当使用 双极性码，PSK发送时，ρ=-1
• 当使用 单极性码，ASK或FSK发送时，ρ=0
• ρ=1时，Pe=0.5，误码率最大

第十一章 同步原理

载波同步

• 插入导频法
• 直接提取法
  • 平方变换法（平方环法）
  • 同相正交环法

位同步

• 外同步法
  • NRZ码：在$\omega_b$处插入导频
  • RZ码，在 $\omega_b/2$ 处插入导频，然后2倍频即可得到 $\omega_b$
• 自同步法
  • 模拟锁相环法
  • 带限整流法
  • 数字锁相环

帧同步

巴克码作帧同步码